日能研に通う小学校5年生の息子が、今週はいろいろな図形の面積の計算に挑戦しています。が、、応用問題の前に、基本的な四角形の性質や面積の算出方法が分かってないことが判明。
図形の難しい問題を解く前に、四角形の種類や性質について正しく理解するとともに、面積の計算方法を身につける必要がありそうなので、一緒に復習してみました。

いつもながら、想定外のスタートラインだ…
1. 四角形の種類と性質
四角形には、台形、平行四辺形、長方形、ひし形、正方形など、いろいろな形のものがあります。
台形は、向かい合う1組の辺が平行という条件だけを満たすものですが、平行四辺形になると向かい合う2組の辺が平行という条件となります。

長方形・ひし形・正方形は、平行四辺形に更に条件が加わった、平行四辺形の特殊な形といえます。

平行四辺形が進化して、長方形・ひし形になるんだね。
ピチューがピカチュウになるようなものか。

あ、平行四辺形の進化先が、長方形とひし形で進化先が分かれてるから、イーブイがブースターとシャワーズに進化するようなものなんだね。

イーブイの場合、性質もノーマルから、炎と水に変化してるから、ちょっと例えは微妙だけど、、、ま、そんな感じ!?
平行四辺形の特殊な形である、長方形になると、全ての角が直角という条件が加わります。
一方、平行四辺形のもう一つの特殊な形であるひし形は、全ての辺の長さが等しいという性質が加わります。
そして、長方形とひし形の性質を併せ持って、全ての角が直角で、全ての辺の長さが等しい、超レアな四角形が「正方形」となります。
学習において、次々と四角形を教えられ、何となくうろ覚えのまま、今まで進んできたわが子のような方もいらっしゃると思いますが、上記のような体系的な整理は、図形の計算問題を解く上で大変重要になります。
2. 四角形の面積の公式
四角形の面積を授業で習ったはずの長男ですが、

台形とひし形って、四角形なのに、なぜ2で割るの?
三角形は半分だから2で割るの分かるけど…
公式を丸暗記してしまうと、忘れた時に応用がきかないので、長男が後で眺められるように、一枚に纏めてみました。

個人指導か家庭教師をつけられれば、親がここまでしなくていいのでしょうが… 早く塾の授業についていけるようになって欲しい

①長方形の面積
長方形の面積は、たて×横なので、この長方形の面積は3cm×4cm=12㎠となります。
三角形は長方形の半分なので、底辺×高さ÷2となります。たては三角形の頂点から底辺に垂直に引いた線の長さを指すので「高さ」と呼びます。
長方形と三角形の面積まではさすがにわが子も理解できていたのですが、次の平行四辺形あたりから怪しくなってきました。
②平行四辺形の面積
底辺が4cm、高さが3cmの平行四辺形の面積は、平行四辺形の端にある三角形を逆方向にくっつけると長方形になることから、長方形と同様に求められます。
ただし、横を底辺と呼び、たては底辺から垂直な長さを指すので「高さ」と呼び、底辺×高さ=4cm×3cm=12㎠となります。
③ひし形の面積
ひし形は、ひし形を囲む長方形を作り、その長方形の半分だと考えます。
ひし形を囲った長方形のたてと横の長さは、ひし形の直角に交わる対角線の長さと等しいので、対角線×対角線÷2 = 4×3÷2 = 6㎠ となります。
④台形の面積
次に上底1cm、下底3cm、高さ3cmの台形の面積を求めます。
台形を上下逆にしたものをもう一つ並べると平行四辺形ができます。
その作られた平行四辺形の底辺は、(上底1cm + 下底3cm) となります。
台形の面積は、平行四辺形の面積の半分なので、台形の面積は(上底+下底)×高さ÷2 =(1cm + 3cm) × 3cm ÷ 2 = 6㎠となります。
3. 正方形の面積を求める問題
最後に正方形の面積を求めてみます。

正方形の面積なんて、一番の基本だよー。よゆうー
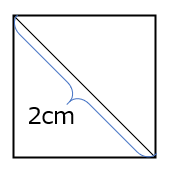

あれ、辺の長さないじゃん。これじゃ、計算できないよ。

対角線はあるよね、正方形って何の進化系だっけ?

おおっ、ひし形か!
そうです! 正方形はひし形の進化系なので、ひし形の計算式でも面積を求めることができます。
対角線×対角線÷2なので、2×2÷2= 2㎠ が答えとなります。
ここまできて、ようやく今週の日能研授業のスタートラインに立つことができました。
栄冠をスタートできるラインに立ててればいいのですが…
4. 四角形の面積 公式のまとめ
さて、四角形の面積の計算方法について学んできましたが、理解できたでしょうか ?
・正方形の面積 = たて×横 (= 対角線×対角線÷2)
・長方形の面積 = たて×横
・平行四辺形の面積 = 底辺×高さ
・ひし形の面積 = 対角線×対角線÷2
・台形の面積 = (上底+下底)×高さ÷2

また一ヵ月後に、計算方法聞くからねー



コメント